I’ve been reading Common Errors in Statistics (and How to Avoid Them) by Phillip Good and James Hardin. It’s a good bathroom/bedtime book. You can pick it up and put it down as you please. Each chapter is self-contained and contains bite-size, easy-to-read sections. I’m really happy with it so far.
Anyway, chapter 3 had a section on computing Power and sample size that inspired me to hop on the computer:
If the data do not come from one of the preceding distributions, then we might use a bootstrap to estimate the power and significance level.
In preliminary trials of a new device, the following test results were observed: 7.0 in 11 out of 12 cases and 3.3 in 1 out of 12 cases. Industry guidelines specified that any population with a mean test result greater than 5 would be acceptable. A worst-case or boundary-value scenario would include one in which the test result was 7.0 3/7th of the time, 3.3 3/7th of the time, and 4.1 1/7th of the time. i.e., \((7 \times \frac{3}{7}) + (3.3 \times \frac{3}{7}) + (4.1 \times \frac{1}{7}) = 5\)
The statistical procedure required us to reject if the sample mean of the test results were less than 6. To determine the probability of this event for various sample sizes, we took repeated samples with replacement from the two sets of test results.
…
If you want to try your hand at duplicating these results, simply take the test values in the proportions observed, stick them in a hat, draw out bootstrap samples with replacement several hundred times, compute the sample means, and record the results.
Well of course I want to try my hand at duplicating the results. Who wouldn’t?
The idea here is to bootstrap from two samples: (1) the one they drew in the preliminary trial with mean = 6.69, and (2) the hypothetical worst-case boundary example with mean = 5. We bootstrap from each and calculate the proportion of samples with mean less than 6. The proportion of results with mean less than 6 from the first population (where true mean = 6.69) can serve as a proxy for Type I error or the significance level. This is proportion of times we make the wrong decision. We conclude the mean is less than 6 when in fact it’s really 6.69. The proportion of results with mean less than 6 from the second population (where true mean = 5) can serve as a proxy for Power. This is proportion of times we make the correct decision. We conclude the mean is less than 6 when in fact it’s really 5.
In the book they show the following table of results:
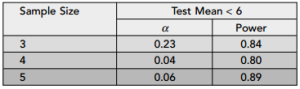
We see they have computed the significance level (Type I error) and power for three different sample sizes. Here’s me doing the same thing in R:
# starting sample of test results (mean = 6.69)
el1 <- c(7.0,3.3)
prob1 <- c(11/12, 1/12)
# hypothetical worst-case population (mean = 5)
el2 <- c(7, 3.3, 4.1)
prob2 <- c(3/7, 3/7, 1/7)
n <- 1000
for (j in 3:5){ # loop through sample sizes
m1 <- double(n)
m2 <- double(n)
for (i in 1:n) {
m1[i] <- mean(sample(el1,j, replace=TRUE,prob=prob1)) # test results
m2[i] <- mean(sample(el2,j, replace=TRUE,prob=prob2)) # worst-case
}
print(paste("Type I error for sample size =",j,"is",sum(m1 < 6.0)/n))
print(paste("Power for sample size =",j,"is",sum(m2 < 6.0)/n))
}
To begin I define vectors containing the values and their probability of occurrence. Next I set n = 1000 because I want to do 1000 bootstrap samples. Then I start the first of two for loops. The first is for my sample sizes (3 - 5) and the next is for my bootstrap samples. Each time I begin a new sample size loop I need to create two empty vectors to store the means from each bootstrap sample. I calls these m1 and m2. As I loop through my 1000 bootstrap samples, I take the mean of each sample and assign to the ith element of the m1 and m2 vectors. m1 holds the sample means from the test results and m2 holds the sample means from the worst-case boundary scenario. Finally I print the results using the paste function. Notice how I calculate the proportion. I create a logical vector by calling mx < 6.0. This returns a vector of 0s and 1s, where 0 is false and 1 is true. I then sum this vector to get the number of times the mean was less than 6. Dividing that by n (1000) gives me the proportion. Here are my results:
[1] "Type I error for sample size = 3 is 0.244" [1] "Power for sample size = 3 is 0.845" [1] "Type I error for sample size = 4 is 0.04" [1] "Power for sample size = 4 is 0.793" [1] "Type I error for sample size = 5 is 0.067" [1] "Power for sample size = 5 is 0.886"
Pretty much the same thing! I guess I could have used the boot function in the boot package to do this. That’s probably more efficient. But this was a clear and easy way to duplicate their results.
One comment