I remember feeling very uncomfortable with the F distribution when I started learning statistics. It comes up when you’re learning ANOVA, which is rather complicated if you’re learning it for the first time. You learn about partitioning the sum of squares, determining degrees of freedom, calculating mean square error and mean square between-groups, putting everything in a table and finally calculating something called an F statistic. Oh, and don’t forget the assumptions of constant variance and normal distributions (although ANOVA is pretty robust to those violations). There’s a lot to take in! And that’s before you calculate a p-value. And how do you do that? You use an F distribution, which when I learned it meant I had to flip to a massive table in the back of my stats book. Where did that table come from and why do you use it for ANOVA? I didn’t know, I didn’t care. It was near the end of the semester and I was on overload.

I suspect this happens to a lot of people. You work hard to understand the normal distribution, hypothesis testing, confidence intervals, etc. throughout the semester. Then you get to ANOVA sometime in late November (or April) and it just deflates you. You will yourself to understand the rules of doing it, but any sort of intuition for it escapes you. You just want to finish the class.

This post attempts to provide an intuitive explanation of what an F distribution is with respect to one-factor ANOVA. Maybe someone will read this and benefit from it.

ANOVA stands for ANalysis Of VAriance. We’re analyzing variances to determine if there is a difference in means between more than 2 groups. In one-factor ANOVA we’re using one factor to determine group membership. Maybe we’re studying a new drug and create three groups: group A on 10 mg, group B on 5 mg, and group C on placebo. At the end of the study we measure some critical lab value. We take the mean of that lab value for the three groups. We wish to know if there is a difference in the means between those three population groups (assuming each group contains a random sample from three very large populations).

The basic idea is to estimate two variances and form a ratio of those variances. If the variances are about the same, the ratio will be close to 1 and we have no evidence that the populations means differ based on our sample.

One variance is simply the mean of the group variances. Say you have three groups. Take the variance of each group and then find the average of those variances. That’s called the mean square error (MSE). In symbol-free mathematical speak, for three groups we have:

MSE = variance(group A) + variance(group B) + variance(group C) / 3

The other variance is the variance of the sample means multiplied by the number of items in each group (assuming equal sample sizes in each group). That’s called mean square between groups (MSB). It looks something like this:

MSB = variance(group means)*(n)

The F statistic is the ratio of these two variances: F = MSB/MSE

Now if the groups have the same means and same variance and are normally distributed, the F statistic has an F distribution. In other words, if we were to run our experiment hundreds and hundreds of times on three groups with the same mean and variance from a normal distribution, calculate the F statistic each time, and then make a histogram of all our F statistics, our histogram would have a shape that can be modeled with an F distribution.

That’s something we can do in R with the following code:

# generate 4000 F statistics for 5 groups with equal means and variances
R <- 4000
Fstat <- vector(length = R)
for (i in 1:R){
  g1 <- rnorm(20,10,4)
  g2 <- rnorm(20,10,4)
  g3 <- rnorm(20,10,4)
  g4 <- rnorm(20,10,4)
  g5 <- rnorm(20,10,4)
  mse <- (var(g1)+var(g2)+var(g3)+var(g4)+var(g5))/5
  M <- (mean(g1)+mean(g2)+mean(g3)+mean(g4)+mean(g5))/5
  msb <- ((((mean(g1)-M)^2)+((mean(g2)-M)^2)+((mean(g3)-M)^2)+((mean(g4)-M)^2)+((mean(g5)-M)^2))/4)*20
  Fstat[i] <- msb/mse
}
# plot a histogram of F statistics and superimpose F distribution (4, 95)
ylim <- (range(0, 0.8))
x <- seq(0,6,0.01)
hist(Fstat,freq=FALSE, ylim=ylim)
curve(df(x,4,95),add=T) # 5 - 1 = 4; 100 - 5 = 95

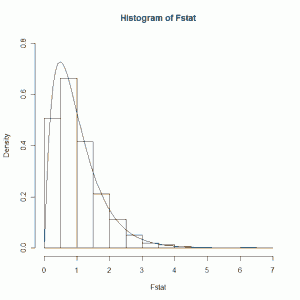
So I have 5 normally distributed groups each with a mean of 10 and standard deviation of 4. I take 20 random samples from each and calculate the MSE and MSB as I outlined above. I then calculate the F statistic. And I repeat 4000 times. Finally I plot a histogram of my F statistics and super-impose a theoretical F distribution on top of it. I get the resulting figure:

This is the distribution of the F statistic when the groups samples come from Normal populations with identical means and variances. The smooth curve is an F distribution with 4 and 95 degrees of freedom. The 4 is Number of Groups - 1 (or 5 - 1). The 95 is from Total Number of Observations - Number of Groups (or 100 - 5). If we examine the figure we see that we most likely get an F statistic around 1. The bulk of the area under the curve is between 0.5 and 1.5. This is the distribution we would use to find a p-value for any experiment that involved 5 groups of 20 members each. When the populations means of the groups are different, we get an F statistic greater than 1. The bigger the differences, the larger the F statistic. The larger the F statistic, the more confident we are that the population means between the 5 groups are not the same.

There is much, much more that can be said about ANOVA. I'm not even scratching the surface. But what I wanted to show here is a visual of the distribution of the F statistic. Hopefully it'll give you a better idea of what exactly an F distribution is when you're learning ANOVA for the first time.